[Lv2] 3장. 도체계 ② 콘덴서의 내압, 절연파괴

 

 

안녕하세요!

 

Lv2 3장 두 번째 포스팅입니다

 

이번 포스팅에서는 

콘덴서의 내압과 절연파괴에 대해

알아보려고 합니다

 

본격적인 내용에 앞서

Lv1에서 콘덴서의 연결에 대해

살펴보았었던 것 기억나시나요

그림으로 공식 잠깐 복습하고

이어가겠습니다

 

 

Lv2에서는

이 콘덴서의 연결 파트에서

직렬연결에 대한 내용을

추가적으로 살펴보려고 합니다

( 문제로 주로 나오는게

직렬연결 부분입니다 )

 

우선적으로

챙겨갈 부분이 하나 있는데요

 

직렬연결에서는

전하량(Q)가 일정하다는

사실입니다

 

회로이론에서

저항의 직렬연결에서는 

전류가 일정하고

 

저항의 병렬연결에서는

전류가 나눠진다는 것을

알고 계신다면

 

'전류'가 '전하의 이동' 을

나타내는 물리량이므로

전하(Q) 또한 동일하게

직렬에서는 일정하고

병렬에서는 나뉜다고 생각하셔도

무방합니다

 

아래 그림처럼

직관적으로 받아들이시면 좋습니다

직렬에서는 전하가 가는 길이

하나라서 나뉘어지지 않으므로

전하량(Q)이 일정합니다

 

 

처음 보면 조금 헷갈릴 수도 있는데

콘덴서는 판 두 개가 세트로 하나의 콘덴서입니다

충전된 전하량도 하나의 세트로 생각해야 합니다

 

한쪽판이 +Q면 반대판은

같은 전하량만큼 -Q로 충전되는데

판이 두 개라 2Q가 되는 것도 아니고

+Q와 -Q가 상쇄되어 0이 되는것도 아니고

그 콘덴서는 그냥 +Q만큼 충전된 콘덴서입니다

 

비교를 위해 병렬도 나타냈고

그림이 복잡해 보일 수 있지만

직렬연결만 보셔도 됩니다

 

회로에서 저항의 직렬연결은

전류가 일정하듯이

콘덴서의 직렬연결에서는

전하량(Q)가 일정하구나

라고 결론만 받아들이면 됩니다

 

 

 

***

 

 

서두에서

Lv2에서는

콘덴서의 연결 파트(직렬과 병렬) 중에서

직렬연결에 대한 추가내용을

살펴보겠다고 했었는데요

 

 

Lv2에서는

평행판 콘덴서를

직렬연결 할 때의

내압과 절연파괴에 대해서

알아보려고 합니다

 

직렬연결은 알겠는데

내압은 뭐고 절연파괴는 또 뭔지

생소할 수 있는데요

 

먼저 콘덴서의 역할을

간단하게 상기해 보면

 

전하를 축적하는 전기 소자

라고 할 수 있습니다

( 콘덴서 또는 커패시터라고 합니다)

 

평행한 두 판에 각각

전하가 모이게 되고

이때 판과 판 사이로 전하가

넘어가지 않아야

제대로 '전하 축적'의 역할을

수행하는 것입니다

 

 

가만히 두 판에 모여있어야 되는데

통과해 지나가버리면

제대로 된 '전하축적' 역할을

수행하지 못하는 거겠죠

(이렇게 전하가 충전된 콘덴서를

활용해 이를 필요로 하는 곳에서

전기적 일을 수행할 수 있는 거죠)

 

콘덴서(또는 커패시터)로 구성된 회로에

전압을 걸어주면 콘덴서에 전하가

모이게 되는데

 

과도하게 전압을 걸어버리면

판과 판 사이에는 흐르지 않던 전류가

흘러버리는 현상이 발생합니다

 

본래 판과 판 사이는 절연상태로

전류가 흐르지 않았는데

전류가 흘러버리는 것으로

이를 콘덴서의 절연파괴 현상이라 합니다

( 콘덴서뿐 아니라 전류가 흐르지 않던 곳에

전류가 흐르는 것을 절연파괴 현상으로 알아두시면 됩니다)

 

 

 

절연이 파괴되어

전류가 흘러버리면

전하가 모이지 않고 흘러가버리니

콘덴서로서의 역할을 수행하지 못하므로

절연파괴가 일어나지 않을 정도로만

전압을 걸어줘야 하는데

 

이때 걸어줄 수 있는 최대전압을

콘덴서가 버틸 수 있는 전압이라 하여

내압이라고 합니다

(안쪽의 전압이 아니라 

버티는 전압이라는 의미네요)

 

 

 

***

 

 

여기까지가 배경 설명이었고

시험에 나오는 부분을

살펴보려고 합니다

 

이 내용에 대해

주로 출제되는 유형이

두 가지가 있습니다

 

1) 콘덴서 여러 개를 직렬연결했을 때

전압이 올라감에 따라

절연이 먼저 파괴되는 콘덴서를 묻는 문제

 

2) 콘덴서 여러개를 직렬연결했을 때

 전체회로의 내압을 묻는 문제

 

 

각 유형의 이론적 설명 이후 강조하게 될

결론부분만 문제에 적용하면 됩니다

 

첫 번째 유형부터 살펴봅시다

 

1) 콘덴서 여러 개를 직렬연결했을 때

전압이 올라감에 따라

절연이 먼저 파괴되는 콘덴서를 묻는 문제

 

예제로 바로 보겠습니다

 

(예제)

 

 

콘덴서를 커패시터라고도 합니다

여러개를 직렬연결하고 전압을 점점 올릴 때

가장 먼저 절연이 파괴되는 것을

묻는 유형입니다

 

위에서 살펴본 내용대로 얼핏 생각하면

콘덴서가 버틸 수 있는 내압을 넘어가면 

절연이 파괴된다고 했으니

 

전압을 서서히 상승시키면

4개 중에 내압이 가장 작은

300V 짜리의 콘덴서가 먼저

파괴되지 않을까 싶은데

꼭 그렇지는 않습니다

 

개별 콘덴서 하나만 따지면

내압이 작은 게 가장 먼저

절연이 파괴되는 게 맞지만,

 

여러 개의 콘덴서를 직렬로 연결하면

정전용량에 따라서 각 콘덴서에

분배되는 전압이 달라지기 때문인데요

 

예를 들어

A콘덴서의 내압이 300V,

B콘덴서의 내압이 600V이지만

A콘덴서에는 200V가 걸리고,

B콘덴서에는 600V가 걸려서

B콘덴서가 먼저 파괴될 수도 있습니다

 

걸리는 전압에 따라서 반대로

A콘덴서가 먼저 파괴될 수도

있는 것이구요

 

따라서 문제에 주어진 내압만으로

단순 비교해서

먼저 파괴되는 콘덴서를

판단하기는 어렵습니다

 

대신에 각 콘덴서에 충전 가능한 

최대 전하량(Q)으로 이를 판단할 수 있습니다

 

전압이 상승하면 그에 따라

충전되는 전하가 많아지게 되는데

충전가능한 최대 전하량을 초과하게 되면

 전압이 더 상승했을 때 버티지 못하고

절연이 파괴되는 것입니다

 

최대 전하량은 어떻게 알 수 있을까요

문제에서 직접 Q가 주어지진 않았지만

Q=CV라는 식을 알고 있기 때문에

각 콘덴서의 정전용량(C)과 내압(V)값을

곱하면 최대 충전 가능한 전하량(Q)를 

알 수 있습니다

 

각 콘덴서의 Q값을 구해보면

 

1000V-2μF 콘덴서 : Q = CV =2×1000 = 2000

700V-3μF 콘덴서 : Q = CV =3×700 = 2100

600V-4μF 콘덴서 : Q = CV = 4×600 = 2400

300V-8μF 콘덴서 : Q = CV = 8×300 = 2400

 

( 정확히는 정전용량 단위가 [μF]이니

각각 $10^{-6}$을 곱해줘야 하지만

모든 콘덴서가 [μF]단위로 동일해서

단순 비교목적의 계산에서는

생략했습니다 )

 

정전용량과 내압을 곱한

Q값이 가장 작은 

1000V-2μF 콘덴서가

가장 먼저 파괴됩니다

 

 

설명이 길었지만 결론적으로 

콘덴서 여러 개를 직렬로 연결할 때

전압을 상승시키면 가장 먼저 파괴되는

콘덴서를 찾는 이런 유형의 문제는

각 콘덴서의 정전용량(C)과 내압(V)을 다 곱해서

가장 작은 걸 찾으면 답이 됩니다

 

 

 

***

 

 

다음으로

 

두 번째 유형인

 

2) 콘덴서 여러개를 직렬연결했을 때

전체회로의 내압을 묻는 문제

 

유형을 보겠습니다

예제를 볼게요

 

(예제)

 

커패시터 3개를 직렬로 연결할 때

전체 내압을 묻는 문제입니다

 

 

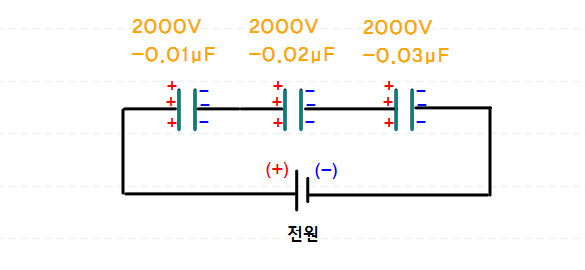
회로이론을 공부하셨다면

직렬연결된 부하에 걸리는 전압은

전압분배 또는 키르히호프 제2법칙에 의해

각각 다 더해주면 전체 전압이 됨을

알 수 있습니다

($V=V_1 + V_2 + V_3$)

 

그러면 각각의 내압이 2.0[kV]이니

전체 내압은 3개를 더해서

6.0[kV]=6000[V]가 될까요? 

그렇지 않습니다

 

그 이유는 위에서 봤던

첫 번째 유형에서 힌트가 있습니다

 

첫 번째 유형이

콘덴서 여러 개를 직렬연결할 때

전압 상승 시 가장 먼저 절연파괴되는

콘덴서를 찾는 거였죠

 

지금의 두 번째 유형에서도 

3개의 콘덴서 내압이

동일하게 2.0[kV]이지만

동시에 절연파괴되는 게 아니라

먼저 절연파괴되는 콘덴서가 있을 것입니다

 

한 개의 콘덴서가 절연파괴가

일어나는 내압인 2.0[kV]에 도달했을 때

나머지 두 콘덴서는 아직

내압인 2.0[kV]에 도달하지 않은 상태인 것입니다

(즉 나머지 두 콘덴서는 2.0[kV]보다 작은 상태이죠)

 

따라서 전체내압은

2.0[kV]+2.0[kV]+2.0[kV]=6.0[kV]가

아니라 6.0[kV]보다 작은 전압이 되어야 합니다

 

하나라도 절연파괴가 일어나면 안 되기에

전압 상승 시 가장 먼저 절연파괴되는 콘덴서를

기준으로 전체 내압을 정해야 하는 것입니다

 

따라서 이번에도 

가장 먼저 파괴되는 콘덴서가

어떤 것인지를 먼저 찾아야 합니다

 

첫 번째 유형에서 봤듯이

정전용량과 내압을 곱한 값이

가장 작은 콘덴서가 먼저 

절연이 파괴되는 콘덴서입니다

 

내압이 2.0[kV]로 동일하고

각각의 정전용량이

0.01[μF], 0.02[μF], 0.04[μF] 이므로

 

Q = CV = 2000×0.01 = 20

Q = CV = 2000×0.02 = 40

Q = CV = 2000×0.04 = 80

 

따라서

전압을 올리다 보면

0.01[μF]의 콘덴서가

먼저 파괴됩니다

 

0.01[μF]의 콘덴서가 

절연파괴가 일어나는 2.0[kV]에 도달했을 때

나머지 두 개는 2.0[kV]가 아닌 것입니다

 나머지 두 콘덴서의 전압이 얼마인지를 알면

2.0[kV]와 나머지 두 전압을 모두 더해주면

전체 내압이 되겠네요

 

나머지 전압을 어떻게 구할까요

Q=CV에서 $V=\frac{Q}{C}$

 

포스팅 초반에 언급했듯이

콘덴서의 직렬연결에서는

Q가 일정하므로

 

V는 $\frac{1}{C}$에 비례합니다

정전용량의 역수에 비례한다는 의미죠

 

따라서 각 콘덴서의 전압의 비를 알기 위해

정전용량의 역수의 비를 따져보면

 

각각의 정전용량이 0.01[μF], 0.02[μF], 0.04[μF] 이므로

역수의 비는

$\frac{1}{0.01}:\frac{1}{0.02}:\frac{1}{0.04}$

입니다

 

분수라서 알아보기 어려우니

분모분자에 각각 100씩 곱해주면

전압의 비는

100:50:25 의 비가 되네요

 ( 첫 번째 콘덴서 전압의 절반이 두번째 콘덴서 전압

첫번째 콘덴서 전압의 1/4이 세 번째 전압인 셈이네요 )

 

0.01[μF], 0.02[μF], 0.04[μF]의 콘덴서에서

0.01[μF]의 전압이 내압에 도달한 2.0[kV]=2000[V] 일 때

0.02[μF]의 전압은 절반인 1.0[kV]=1000[V]

0.04[μF]의 전압은 1/4인 0.5[kV]=500[V]가 됩니다

 

심플하게

전압 V가 정전용량 C에 반비례하므로

0.01[μF] 콘덴서가 2000[V]일 때를 기준으로

0.02[μF] 콘덴서는 정전용량이 2배니 

전압은 반대로 1/2이 되어 1000[V]

0.04[μF] 콘덴서는 정전용량이 4배니

전압은 반대로 1/4이 되어 500[V]

이렇게 볼 수도 있겠네요

 

따라서 세 전압을 다 더해주면

2000+1000+500=3500[V]

3500[V]가 전체내압이 됩니다

 

 

전체회로에 3500V를 걸어주면

0.01[μF]의 콘덴서가 2.0[kV]에 도달해

절연이 파괴되는 것입니다

 

 

복잡한 것 같지만 결론적으로 

① 각 콘덴서의 정전용량(C)과 내압(V)을 다 곱해서

가장 작은 콘덴서(먼저 절연파괴되는 콘덴서)를 먼저 찾고

 

② 해당 콘덴서의 전압이 내압에 도달했다고 가정하고

그때의 나머지 콘덴서들의 전압을 찾기 위해

각 정전용량의 역수의 비를 이용합니다

( 위에서 본 것처럼 심플하게

먼저 파괴되는 콘덴서의 정전용량과

반비례함을 이용해 구할 수도 있습니다 )

 

③ 구한 3개의 전압을

다 더해주면 전체 내압이 됩니다

 

 

내용설명은 여기까지입니다

설명을 위해 길어졌지만

문제를 풀다 보면 절차적으로

숙달되실 거라 생각합니다

 

 

 

 

***

 

 

 

문제 풀어보겠습니다

 

(문1)

(풀이)

 

최초로 파괴되는 콘덴서를 

묻는 유형의 문제입니다

콘덴서 3개를 직렬로

연결한 상황이네요

 

 

위에서 설명은 길게 했지만

결론적으로

각각의 내압과 정전용량을 곱해

가장 작은 콘덴서가

먼저 파괴된다고 했었습니다

 

1000×1=1000

750×2=1500

500×5=2500

 

이므로 곱한 값이 1000으로 가장 작은

1[μF] 콘덴서가 가장 먼저 파괴됩니다

 

 

답은 ①번입니다

 

답) ①

 

 

 

 

(문2)

(풀이)

 

콘덴서의 내압을 구하는 문제입니다

3개의 콘덴서를 직렬로 연결한 상황이네요

 

 

내압을 구하는 문제에서도 역시

가장 먼저 절연파괴되는 콘덴서를 

찾아야 한다고 했습니다

 

1000×0.01 = 10

1000×0.02 = 20

1000×0.04 = 30

 

이므로

0.01 [μF] 콘덴서가 

가장 먼저 절연파괴됩니다

 

그 말은

0.01 [μF] 콘덴서가 내압인

1[kV]에 먼저 도달한다는 의미이므로

해당 콘덴서의 전압이 1[kV] =1000[V]라고 두고

나머지 두 콘덴서의 전압을 구해서 더해주면 됩니다

 

전압의 비가 정전용량의 역수의 비와 같으므로

정전용량의 역수의 비는

$\frac{1}{0.01}:\frac{1}{0.02}:\frac{1}{0.04}$

 

분수라서 알아보기 어려우니

분모분자에 각각 100씩 곱해주면

전압의 비는

100:50:25 의 비가 되네요

 ( 첫번째 콘덴서 전압의 절반이 두번째 콘덴서 전압

첫번째 콘덴서 전압의 1/4이 세 번째 전압인 셈이네요 

 

0.01[μF], 0.02[μF], 0.04[μF]의 콘덴서에서

0.01[μF]의 전압이 내압에 도달한 1.0[kV]=1000[V] 일때

0.02[μF]의 전압은 절반인 500[V]

0.04[μF]의 전압은 1/4인 250[V]가 됩니다

 

심플하게

전압 V가 정전용량 C에 반비례하므로

0.01[μF] 콘덴서가 1000[V]일 때를 기준으로

0.02[μF] 콘덴서는 정전용량이 2배니 

전압은 반대로 1/2이 되어 500[V]

0.04[μF] 콘덴서는 정전용량이 4배니

전압은 반대로 1/4이 되어 250[V]

이렇게 볼 수도 있겠네요

 

따라서 세 전압을 다 더해주면

1000+500+250=1750[V]

1750[V]가 전체내압이 됩니다

 

 

내압 구하는 예제와

풀이과정이 너무 비슷하다는 게 

보이시나요

 

해당 예제와 이번 문제가 

주어진 내압만 2[kV]와 1[kV]로 다르고

나머지 주어진 정전용량이 동일합니다

 

둘 다 기출 된 문제인데

숫자만 살짝 다르게 출제된것이네요

 

과년도 기출문제를 풀다가

같은 문제라 생각해서 하나의 답만 외웠다가는 

틀릴 수 있으니 내압계산과정을

생각해보아야 하는 유형입니다

 

답) ①

 

 

 

 

(문3)

(풀이)

 

가장 먼저 절연이 파괴되는

콘덴서를 묻는 문제입니다

 

이번에는 내압과 정전용량을

곱하는 문제가 아니라

말로 물어보았네요

 

주어진 내압만으로 단순비교해서

먼저 파괴되는 콘덴서를 판단하기는 어렵지만

 

대신에 각 콘덴서에 충전 가능한 

최대 전하량(Q)으로 이를 판단할 수 있다고

위에서 언급한 바 있습니다

 

 

보기에 

최대 충전 전하량이 가장 작은 콘덴서라는

내용이 있는 ②번이 답이 됩니다

 

답) ②

 

 

연습문제까지

풀어보았습니다!

 

 

***

 

 

 

<요약>

 

 

 

Lv2 3장 2번째 포스팅은

여기까지입니다

 

콘덴서의 직렬연결 시

절연파괴와 회로 내압에 대한 내용을

살펴보았네요

 

배경 설명이 길어져 

 힘드시지는 않으셨을지

모르겠습니다

 

문제 푸는 요령만 건지셔도

충분한 내용입니다

 

해당 문제유형을 몇번 보고

풀이과정이 숙달되면

특히나 가장 먼저파괴되는 콘덴서를

찾는 문제는 몇 초 안에 답을 찾아낼수도

있을 것이라 생각합니다

 

전체내압을 구하는 부분이 조금

복잡하긴 하지만 정형화된 유형이라

반복을 통해 풀이과정이 암기되는 수준이

된다면 더욱 수월해질 거라 생각합니다

 

다음 포스팅에서는

Lv2 3장 중 정전에너지 등

나머지 내용을 다뤄보겠습니다

 

감사합니다!